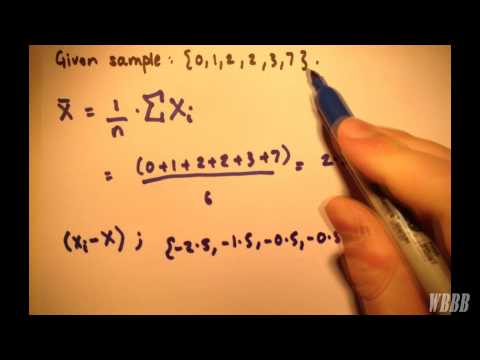
Sadržaj
- 1. korak: izračunajte prosječnu vrijednost uzorka
- 2. korak: oduzmite srednju vrijednost od pojedinačnih vrijednosti
- Korak 3: Kvadrati pojedinačne varijacije
- Korak 4: Dodajte kvadrate odstupanja
- Runda bonusa
Pojmovi poput značiti i odstupanje su za statistiku što su tijesto, paradajz sos i sir mocarela za pizzu: U principu je jednostavno, ali imate toliko različitih međusobno povezanih primjena da je lako izgubiti trag od osnovne terminologije i redoslijeda kojim morate obavljati određene operacije.
Izračunavanje zbrajanja kvadratnih odstupanja od srednje vrijednosti uzorka korak je na putu izračunavanja dvije vitalne opisne statistike: varijancu i standardno odstupanje.
1. korak: izračunajte prosječnu vrijednost uzorka
Da biste izračunali srednju vrijednost (koja se često naziva prosjek), dodajte pojedinačne vrijednosti uzorka zajedno i podijelite s n, ukupnih predmeta u uzorku. Na primjer, ako vaš uzorak uključuje pet rezultata kviza, a pojedinačne vrijednosti su 63, 89, 78, 95 i 90, zbroj tih pet vrijednosti je 415, a srednja vrijednost je stoga 415 ÷ 5 = 83.
2. korak: oduzmite srednju vrijednost od pojedinačnih vrijednosti
U ovom primjeru, srednja vrijednost je 83, tako da ovaj postupak oduzimanja daje vrijednosti (63-83) = -20, (89-83) = 6, (78-83) = -5, (95-83) = 12 , i (90-83) = 7. Te se vrijednosti nazivaju odstupanja, jer opisuju stupanj odstupanja svake vrijednosti od uzorka.
Korak 3: Kvadrati pojedinačne varijacije
U ovom slučaju, kvadrat -20 daje 400, četvrtanje 6 daje 36, četvrtanje -5 daje 25, četvrtanje 12 daje 144, a četvrtanje 7 daje 49. Ove vrijednosti su, kao što biste i očekivali, kvadrat odstupanja utvrđenih u prethodnom korak.
Korak 4: Dodajte kvadrate odstupanja
Da biste dobili zbroj kvadrata odstupanja od srednje vrijednosti i time dovršili vježbu, dodajte vrijednosti koje ste izračunali u koraku 3. U ovom primjeru ta je vrijednost 400 + 36 + 25 + 144 + 49 = 654. Zbroj od kvadrata odstupanja često se skraćuje SSD u statističkom jeziku.
Runda bonusa
Ovom vježbom se najveći dio posla uključuje izračun varijance uzorka, koji je SSD podijeljen s n-1, i standardno odstupanje uzorka, što je kvadratni korijen varijance.