Sadržaj
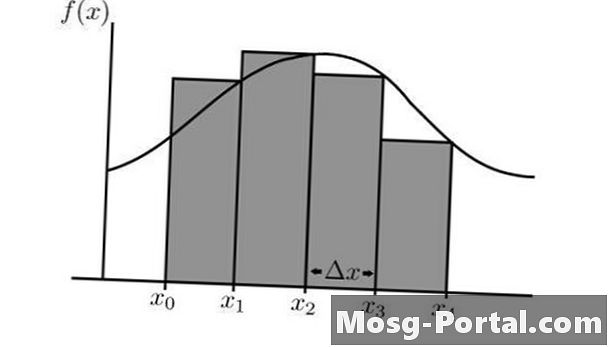
Riemannova suma aproksimacija je područja ispod matematičke krivulje između dvije vrijednosti X. Ovo se područje aproksimira korištenjem niza pravokutnika koji imaju odabranu širinu delte X i visinu koja je izvedena iz dotične funkcije, f (X). Što je delta X manja, to će aproksimacija biti točnija. Visina se može uzeti iz vrijednosti f (X) bilo s desne, srednje ili lijeve strane pravokutnika. Možete naučiti kako izračunati lijevu Riemannovu svotu.
Pronađite vrijednost f (X) kod prve X vrijednosti. Kao primjer uzmimo funkciju f (X) = X ^ 2, a aproksimiramo područje ispod krivulje između 1 i 3 s deltom X od 1; 1 je prva X vrijednost u ovom slučaju, pa je f (1) = 1 ^ 2 = 1.
Pomnožite visinu, kao što je pronađeno u prethodnom koraku, s deltom X. Time ćete dobiti područje prvog pravokutnika. Na primjer, 1 x 1 = 1.
Prvoj X vrijednosti dodajte delta X. Tako ćete dobiti vrijednost X na lijevoj strani drugog pravokutnika. Na primjer, 1 + 1 = 2.
Ponovite gornje korake za drugi pravokutnik. Nastavljajući primjer, f (2) = 2 ^ 2 = 4; 4 x 1 = 4. Ovo je područje drugog pravokutnika u primjeru. Nastavite na ovaj način dok ne postignete konačnu X vrijednost. Na primjer, postoje samo dva pravokutnika jer je 2 +1 = 3, što je kraj raspona koji se mjeri.
Dodajte područje svih pravokutnika. Ovo je Riemannova svota. Završavajući primjer, 1 + 4 = 5.