
Sadržaj
Da bi dva oblika bila skladna, svaki mora imati isti broj strana, a njihovi kutovi također moraju biti isti. Najlakši način da se utvrdi da li su dva oblika jednaka je rotiranje jednog oblika dok se ne slože s drugim ili jednostavno složite oblike jedan na drugi kako bi se vidjelo izlaze li neki krajevi. Ako niste u mogućnosti fizički pomicati oblike, pomoću formula možete utvrditi da li su oblici skladni.
Kongruentni krugovi
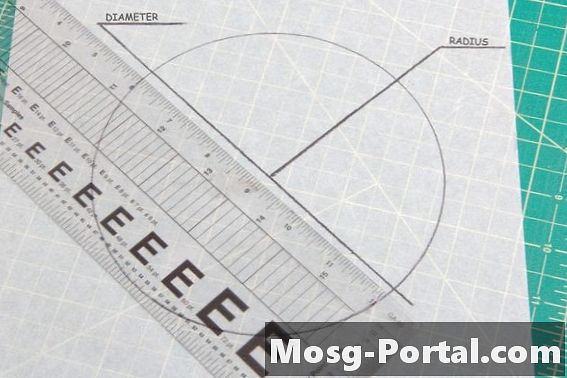
••• Ray Robert Green / Mediji potražnjeSvi krugovi imaju isti kut od 360 stupnjeva. Jedini čimbenik u određivanju kongruencije dvaju krugova je usporedba njihove veličine. Promjer je ravna linija kroz sredinu kruga od ruba do ruba, dok je polumjer kruga duljina od njegovog središta do vanjskog ruba. Ako je mjerenje oba u oba kruga dokazano, jesu li u skladu.
paralelograma
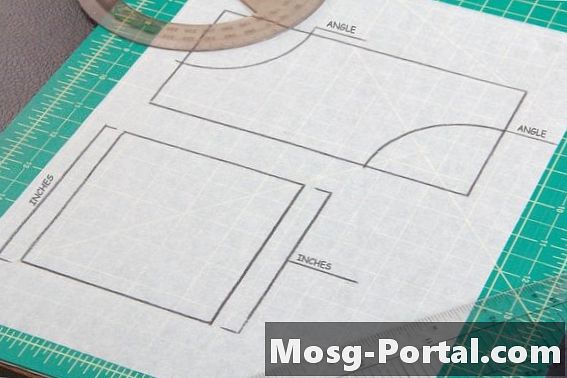
Paralelogram ima dva para paralelnih strana, poput kvadrata i pravokutnika. Suprotne strane ili kutovi paralelograma imaju istu mjeru, pa je potrebno uzeti dva kuta ili bočna mjerenja na paralelogramu, po jedno sa svakog para strana, kako bi se usporedila kongruencija s drugim oblikom.
trokuti
••• Ray Robert Green / Mediji potražnjeDa biste pronašli kongruenciju trokuta, morate odrediti veličinu svakog kuta ili strane, jer sva tri mogu biti različita. Postoje tri postulata pomoću kojih se mogu identificirati ujednačeni trokuti. SSS postulat je kada odmjerite sve tri strane u svaki trokut. AS-ov postulat kaže ako se bilo koji kut i njihova spojna strana podudaraju s onim u drugom trokutu, tada su oni sukladni. SAS postulat čini suprotno, mjereći dvije strane i njihov spojni kut za usporedbu s drugim trokutom.
Teoreme za kongruentne trokute

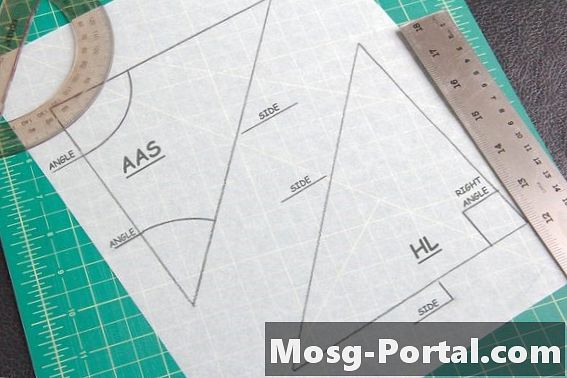
Dvije teoreme korisne su za pronalaženje složenih trokuta. Teorema AAS kaže da ako su dva kuta i strana koja ih ne spaja jednaka onoj drugog trokuta, tada su one jednake. Teorem Hypotenuse-Leg odnosi se samo na trokut s jednim kutom od 90 stupnjeva ili "pravom". To je slučaj kada izmjerite hipotenuzu - stranu suprotnu kutu od 90 stupnjeva - i jednu od drugih strana trokuta, za usporedbu s drugim oblikom.