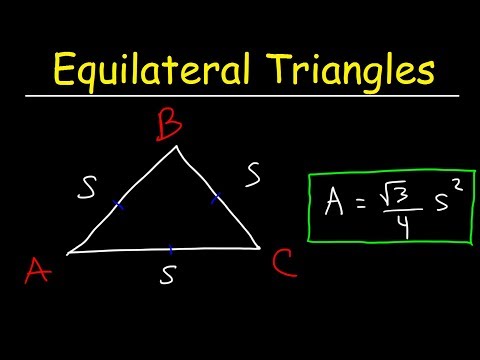
Jednakostrani trokut je trokut sa sve tri strane jednake duljine. Površina dvodimenzionalnog poligona, poput trokuta, ukupna je površina sadržana na stranama poligona. Tri kuta jednakostraničnog trokuta također su jednaka mjera u euklidskoj geometriji. Budući da je ukupna mjera kutova euklidskog trokuta 180 stupnjeva, to znači da svi kutovi jednakostraničnog trokuta mjere 60 stupnjeva. Površina jednakostraničnog trokuta može se izračunati kada je poznata duljina jednog od njegovih strana.

Odredite područje trokuta kada su poznata baza i visina. Uzmimo bilo koja dva identična trokuta s osnovom s i visinom h. Uvijek možemo stvoriti paralelogram baze s i visine h s ova dva trokuta. Budući da je područje paralelograma s x h, područje A trokuta je dakle ½ s x h.

Pravokutni trokut formirajte u dva prava trokuta s linijskim segmentom h. Hipotenuza jednog od ovih desnih trokuta duljine s, jedna je noga duljine h, a druga noga duljine s / 2.
Izrazite h u smislu s. Koristeći pravi trokut formiran u koraku 2, znamo da je s ^ 2 = (s / 2) ^ 2 + h ^ 2 po pitagorejskoj formuli. Stoga je h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, a sada imamo h = (3 ^ 1/2) s / 2.
Vrijednost h dobivenu u koraku 3 zamijenite formulom za područje trokuta dobivenog u koraku 1. Budući da je A = ½ sxh i h = (3 ^ 1/2) s / 2, sada imamo A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Upotrijebite formulu za područje jednakostraničnog trokuta dobivenog u koraku 4 da biste pronašli područje jednakostraničnog trokuta sa stranicama duljine 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).