Elipsa se u geometriji ravnine može definirati kao skup točaka tako da je zbroj njihovih udaljenosti do dvije točke (žarišta) konstantan. Rezultirajući lik može se matematički opisati i kao ovalni ili "spljošteni krug". Elipsa ima niz primjena u fizici i osobito je korisna u opisivanju planetarnih orbita. Ekscentričnost je jedna od karakteristika i elipse i mjeri koliko je kružne elipse.
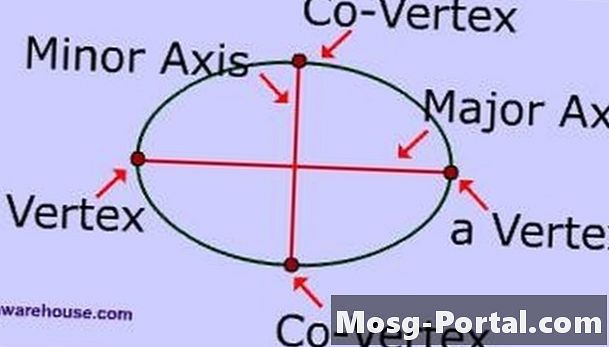
Ispitajte dijelove elipse. Glavna os je najduži linijski segment koji presijeca sredinu elipse i ima svoje krajnje točke na elipsi. Manja os je najkraći linijski segment koji presijeca sredinu elipse i ima svoje krajnje točke na elipsi. Glavna poluosna je polovina glavne osi, a mala poluosna polovica manje osi.
Ispitajte formulu elipse. Postoji mnogo različitih načina matematičkog opisivanja elipse, ali za izračunavanje ekscentričnosti najviše je korisno za elipsu: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konstante a i b su specifične za određenu elipsu, a varijable su x i y koordinate točaka koje leže na elipsi. Ova jednadžba opisuje elipsu sa središtem u početku i glavnim i manjim osovinama koje leže na izvorima x i y.
Odredite duljine poluosi. U jednadžbi x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, duljine poluosi su date sa a i b. Veća vrijednost predstavlja glavnu poluosu, a manja vrijednost manje poluosi.
Izračunajte položaje žarišta. Fokusi su smješteni na glavnoj osi, po jednu sa svake strane središta. Budući da osi elipse leže na linijama podrijetla, jedna koordinata bit će 0 za obje žarišta. Druga koordinata za će biti (a ^ 2 - b ^ 2) ^ (1/2) za jedno žarište i - (a ^ 2 - b ^ 2) ^ (1/2) za ostale žarišta gdje je a> b.
Izračunajte ekscentričnost elipse kao omjer udaljenosti fokusa od središta i duljine polu-glavne osi. Ekscentričnost e je dakle (a ^ 2 - b ^ 2) ^ (1/2) / a. Imajte na umu da je 0 <= e <1 za sve elipse. Ekscentričnost 0 znači da je elipsa krug, a dugačka tanka elipsa ima ekscentričnost koja se približava 1.