Sadržaj
Izračunavanje vjerojatnosti zahtijeva pronalaženje različitog broja ishoda za događaj --- ako bacate novčić 100 puta, imate 50 posto vjerojatnosti okretanja repova. Normalna raspodjela je vjerojatnost raspodjele među različitim varijablama i često se naziva Gaussovom raspodjelom. Normalna raspodjela predstavljena je zvonastom krivuljom, gdje je vrh krivulje simetričan oko srednje vrijednosti jednadžbe. Izračunavanje vjerojatnosti i normalne raspodjele zahtijeva poznavanje nekoliko određenih jednadžbi.
Vjerojatnost
Zapišite jednadžbu za vjerojatnost: p = n / N. "n" označava povoljne elemente, a "N" stoji za postavljene elemente. Za ovaj primjer, recimo da imate 20 jabuka u vrećici. Od 20 jabuka, pet je zelenih jabuka, a preostalih 15 je crvenih jabuka. Ako posegnete za torbom, kolika je vjerojatnost da ćete pokupiti zelenu?
Postavljanje jednadžbe:
p = 5/20
Podijelite 5 na 20:
5 / 20 = 0.25
Imajte na umu da ishod nikada ne može biti jednak ili veći od 1.
Pomnožite 0,25 sa 100 da biste dobili svoj postotak:
p = 25 posto
Šanse da zgrabite zelenu jabuku iz vrećice s 15 crvenih jabuka su 25 posto.
Normalna distribucija
Zapišite jednadžbu za normalnu raspodjelu: Z = (X - m) / Standardno odstupanje.
Z = Z tablica (vidi Resursi) X = Normalna slučajna varijabla m = srednja vrijednost ili prosjek
Recimo da želite pronaći normalnu raspodjelu jednadžbe kada je X 111, srednja je 105 a standardna devijacija je 6.
Postavljanje jednadžbe:
Z = (111 - 105) / 6
Oduzmi 111 od 105:
Z = 6/6
Podijelite 6 na 6:
Z = 1
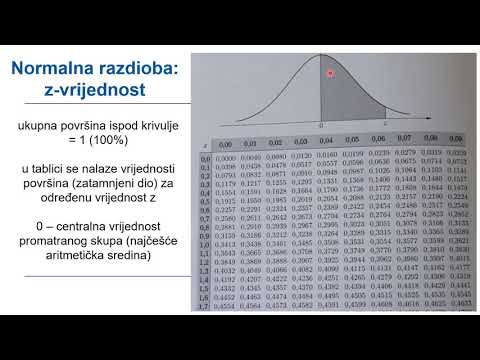
Potražite vrijednost 1 iz tablice Z (pogledajte Resursi):
Z = 1 = 0,3413 Budući da je vrijednost X (111) veća od srednje vrijednosti (105) na početku jednadžbe, dodaćete 0,5 do Z (0,3413). Ako je vrijednost X bila manja od srednje, od Z. oduzmete 0,5.
0.5 + 0.3413 = 0.8413
Stoga je 0,8413 vaš odgovor.