
Sadržaj
U geometriji je osmerokut mnogokut s osam strana. Pravi osmerokut ima osam jednakih strana i jednakih kutova. Regularni osmerokut je obično prepoznat iz znakova zaustavljanja. Oktaedar je osmerostrani poliedar. Obični oktaedar ima osam trokuta s rubovima jednake duljine. Učinkovito se dvije kvadratne piramide sastaju u njihovim bazama.
Formula područja oktagona
Formula za područje pravilnog osmerokuta sa stranicama duljine "a" je 2 (1 + sqrt (2)) a ^ 2, gdje "sqrt" označava kvadratni korijen.
derivacija
Osmerokut se može gledati kao 4 pravokutnika, jedan kvadrat u središtu i četiri izoscele trokuta u uglovima.
Kvadrat je površine a ^ 2.
Trokut ima stranice a, a / sqrt (2) i a / sqrt (2), pitagorejskim teoremom. Stoga, svaki ima područje ^ 2/4.
Pravokutnici su površine a * a / sqrt (2).
Zbroj ovih 9 područja je 2a ^ 2 (1 + sqrt (2)).
Formula volumena oktaedra
Formula volumena pravilnog oktaedra strana "a" je ^ 3 * sqrt (2) / 3.
derivacija
Područje četverostrane piramide je područje baze * visina / 3. Područje pravilnog osmerokuta je 2 * osnovica * visina / 3.
Baza = a ^ 2 trivijalno.
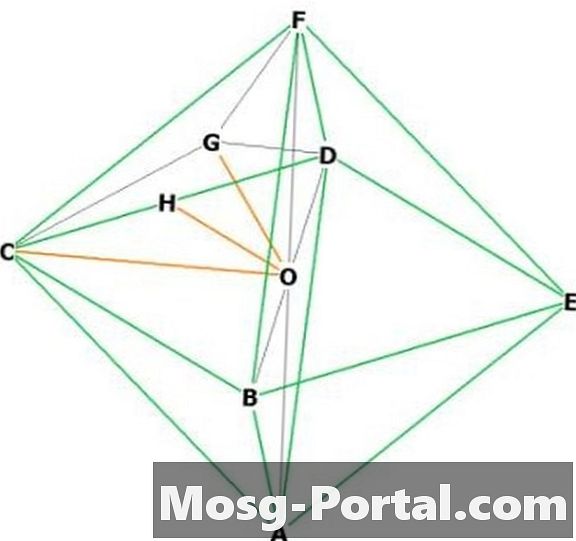
Odaberite dvije susjedne vrhove, recite "F" i "C." "O" je u središtu. FOC je isoscelesni desni trokut s bazom "a", pa su pitagorejski teoremi OC i OF duljine a / sqrt (2). Dakle, visina = a / sqrt (2).
Dakle, volumen pravilnog oktaedra je 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Površina
Uobičajena površina oktaedra je područje jednakostraničnog trokuta strane "a", puta 8 lica.
Da biste upotrijebili pitagorejski teorem, ispustite crtu od vrha do baze. To stvara dva prava trokuta, s hipotenuzom duljine "a" i jedne bočne duljine "a / 2". Stoga treća strana mora biti sqrt = sqrt (3) a / 2. Dakle, područje jednakostraničnog trokuta je visina * osnova / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
S 8 strana površina površine pravilnog oktaedra je 2 * sqrt (3) * a ^ 2.